Geneva Mechanism

A Geneva Mechanism (otherwise known as Maltese Cross) is used to turn continuous rotary motion to intermittent motion. It looks like this:

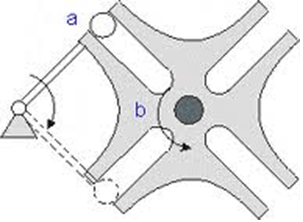
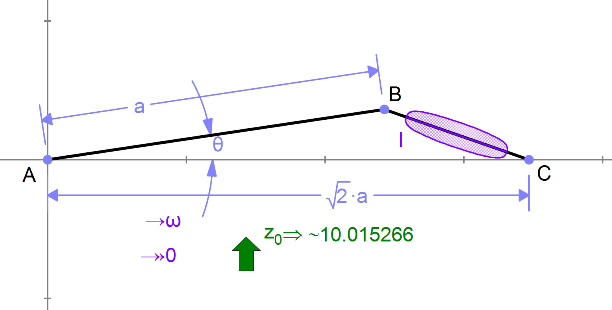
Member A rotates continuously, while B rotates 90 degrees at a time.

We’d like to compute the maximum torque required, assuming b has moent of inertia I.

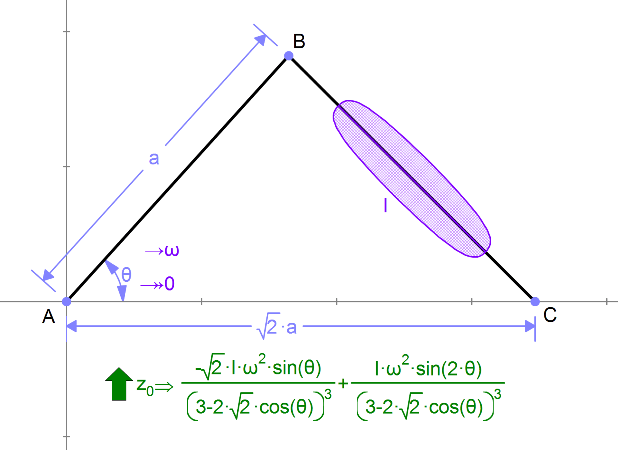
Setting I and ω to 1, we can graph this:

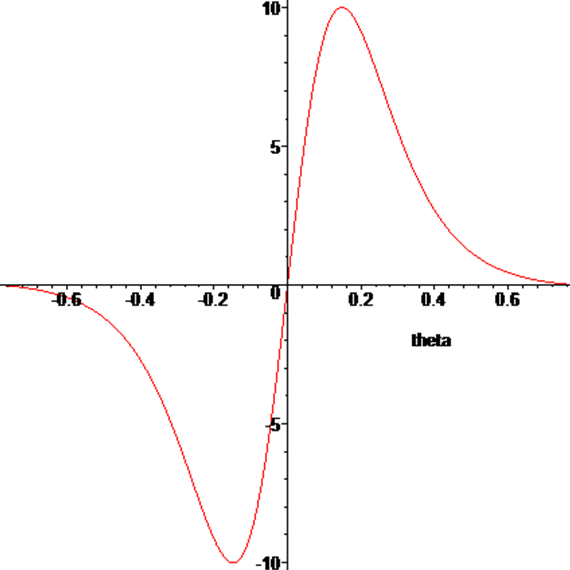
To find the maximum’s location, we can differentiate:

>simplify(diff(u,theta));

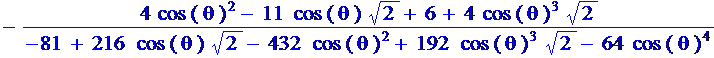
Solving (numerically) for θ gives:

>solve(du=0,theta);

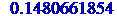
We can set the numeric value of θ in the variable panel, and look at the numeric reaction torque to get our maximal value (or we could have read off the graph above).