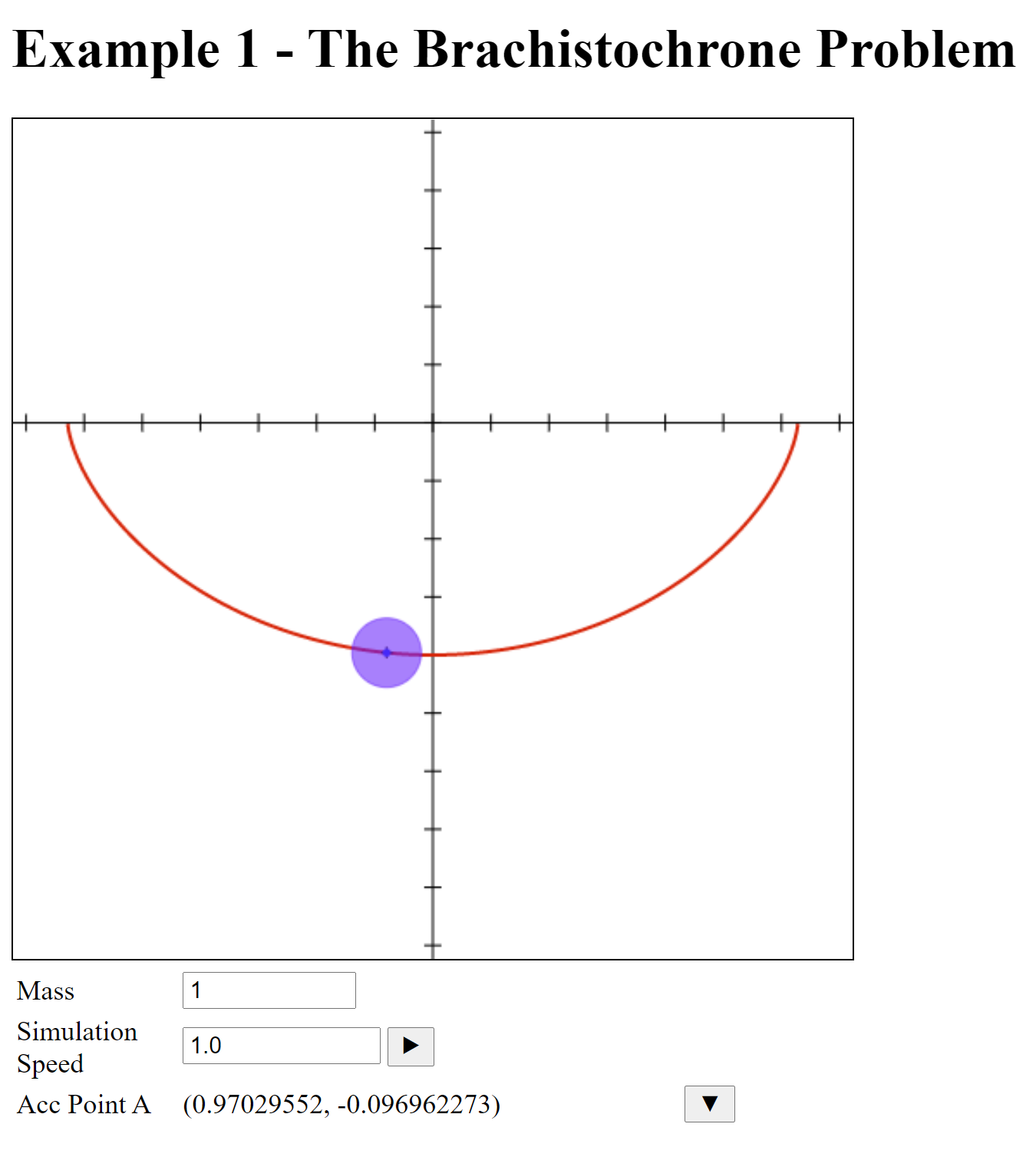
An inverted cycloid curve is the solution to the brachistochrone problem: providing the quickest path between two points for a ball rolling under gravity, or a bead sliding on a wire. You can find this model and run the app (Example 23) in the Examples subdirectory of your Mx installation.
Here are the steps to create the model:
- Select Draw / Function
and choose Parametric from the Type window. - Enter: X = T+sin(T), Y = -1-cos(T) with T varying from -3.14 to 3.14.
- Draw / Point
on the curve. - Select the point and the curve and choose Point Proportional from the Constrain toolbox
with a value of t. - Select the parameter t and right-click to get the Context menu and choose Free Constraint to Accelerate.
- To see the acceleration of the point over time,
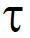, select the point and click Velocity / Acceleration from the Mechanics Output toolbox 
.
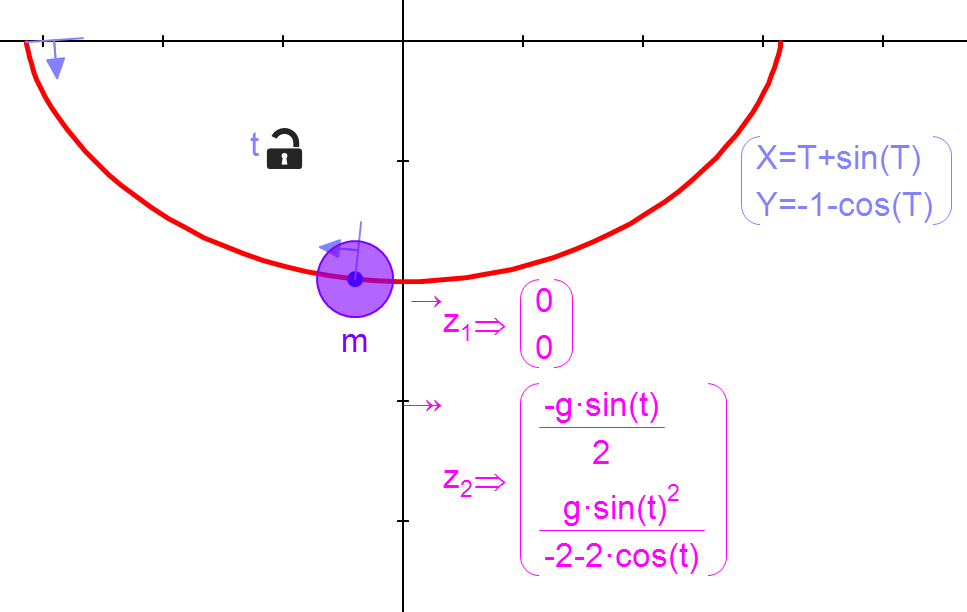
Your model should appear like this:
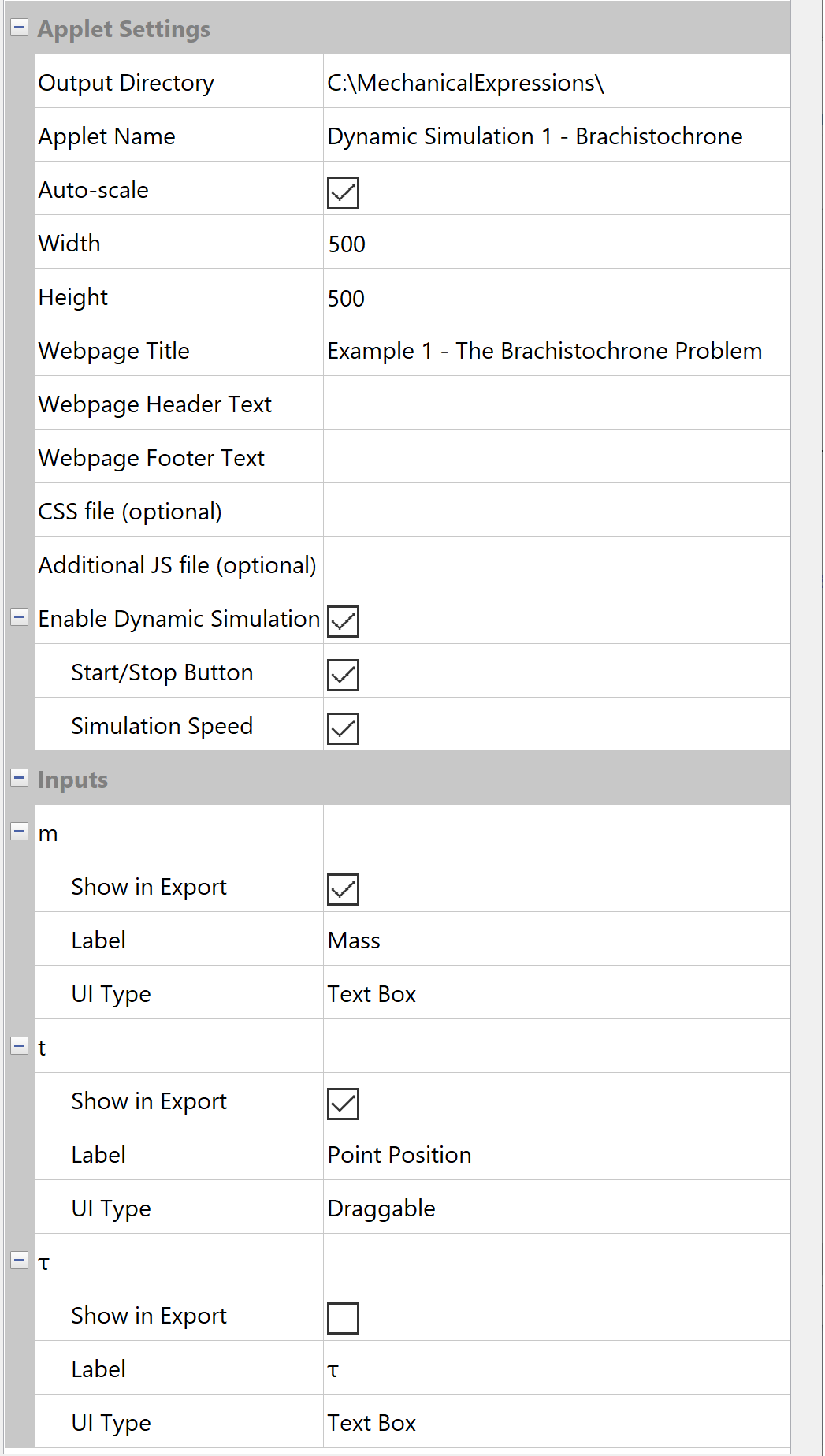
Now you are ready to Export / HTML5 / Javascript App, found in the File menu.
- Specify that the app should contain a simulation, give it a start button (the default has these checked), and set t to be draggable. In the dialog below, we also clarify the labels.
You can drag the point along the curve and see its change in acceleration. Click the down arrow in the acceleration line to see a graph Click the arrow again to see the table of the output. The App looks like this:
